Randomizes a raster stack with fixed richness and species frequency of incidence. Randomizations are based on frequencies (given or calculated from x) and, optionally, a probability raster stack. The probability raster stack controls the probability that a given species is sampled in each cell raster. Frequency controls the number of cells being sampled for each species.
Usage
bootspat_ff(
x,
rprob = NULL,
rich = NULL,
fr = NULL,
glob_fr = NULL,
cores = 1,
filename = "",
overwrite = FALSE,
...
)Arguments
- x
SpatRaster. A presence-absence SpatRaster.
- rprob
SpatRaster. Stack of probability values. Structures the spatial pattern of each randomized species.
- rich
SpatRaster. Richness pattern structuring the sample size of each cell randomization. Calculated if not provided.
- fr
The observed frequency of incidence (i.e. number of occupied pixels) of each species is across the study area.
- glob_fr
The size (i.e. number of pixels) of the study area.
- cores
positive integer. If
cores > 1, a 'parallel' package cluster with that many cores is created and used. You can also supply a cluster object. Ignored for functions that are implemented by terra in C++ (see under fun)- filename
character. Output filename
- overwrite
logical. If
TRUE,filenameis overwritten- ...
additional parameters for terra::app
Details
The algorithm is based on the algorithm of Connor & Simberloff (1979). It takes each species at a time and placed on Nj (species frequency of incidence) randomly chosen sites (cells). The original algorithm randomly chooses the sequence of species and fills sites (originally islands) until they reach the observed species richness. However, as sites (cells) are filled with species, some species do not have enough available sites to be placed, and their sampled frequency is smaller than observed. Additionally, some sites cannot be completely filled because duplicated species are not allowed in the same site. Their solution was to increase the number of sites to place the species. Here, we opted to order the sequence of species from the largest Nj to the smallest. Also, the probability of occupying a site is given by cell expected richness and on each round (i.e. species placement), the expected richness of newly occupied sites is reduced. This ensures that there will be available sites for all species and the randomized frequency of incidence equals the observed frequency of incidence (Nj).
References
Connor, E. F., & Simberloff, D. (1979). The Assembly of Species Communities: Chance or Competition? Ecology, 60(6), 1132–1140.
Examples
# load random species distributions
library(SESraster)
library(terra)
r <- load_ext_data()
plot(r)
 # applying the function
rand.str <- bootspat_str(r)
plot(rand.str)
# applying the function
rand.str <- bootspat_str(r)
plot(rand.str)
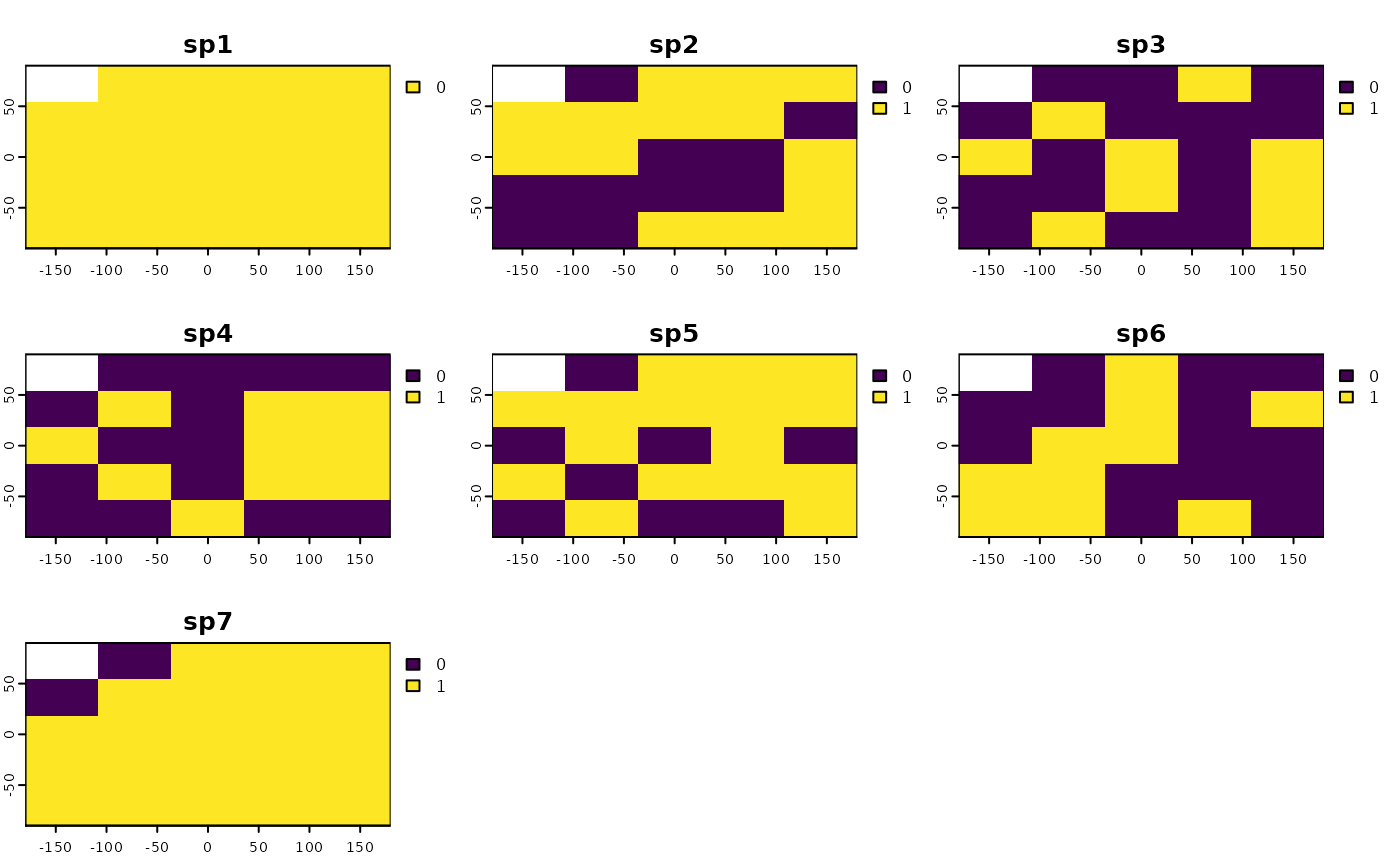 # With null probability raster
rprobnull <- terra::app(r,
function(x){
ifelse(is.na(x), NA, 1)
})
rand.str2 <- bootspat_str(r, rprob = rprobnull)
library(SESraster)
library(terra)
# creating random species distributions
f <- system.file("ex/elev.tif", package="terra")
r <- rast(f)
set.seed(510)
r10 <- rast(lapply(1:8,
function(i, r, mn, mx){
app(r, function(x, t){
sapply(x, function(x, t){
x<max(t) & x>min(t)
}, t=t)
}, t=sample(seq(mn, mx), 2))
}, r=r, mn=minmax(r)[1]+10, mx=minmax(r)[2]-10))
names(r10) <- paste("sp", 1:nlyr(r10))
plot(r10)
# With null probability raster
rprobnull <- terra::app(r,
function(x){
ifelse(is.na(x), NA, 1)
})
rand.str2 <- bootspat_str(r, rprob = rprobnull)
library(SESraster)
library(terra)
# creating random species distributions
f <- system.file("ex/elev.tif", package="terra")
r <- rast(f)
set.seed(510)
r10 <- rast(lapply(1:8,
function(i, r, mn, mx){
app(r, function(x, t){
sapply(x, function(x, t){
x<max(t) & x>min(t)
}, t=t)
}, t=sample(seq(mn, mx), 2))
}, r=r, mn=minmax(r)[1]+10, mx=minmax(r)[2]-10))
names(r10) <- paste("sp", 1:nlyr(r10))
plot(r10)
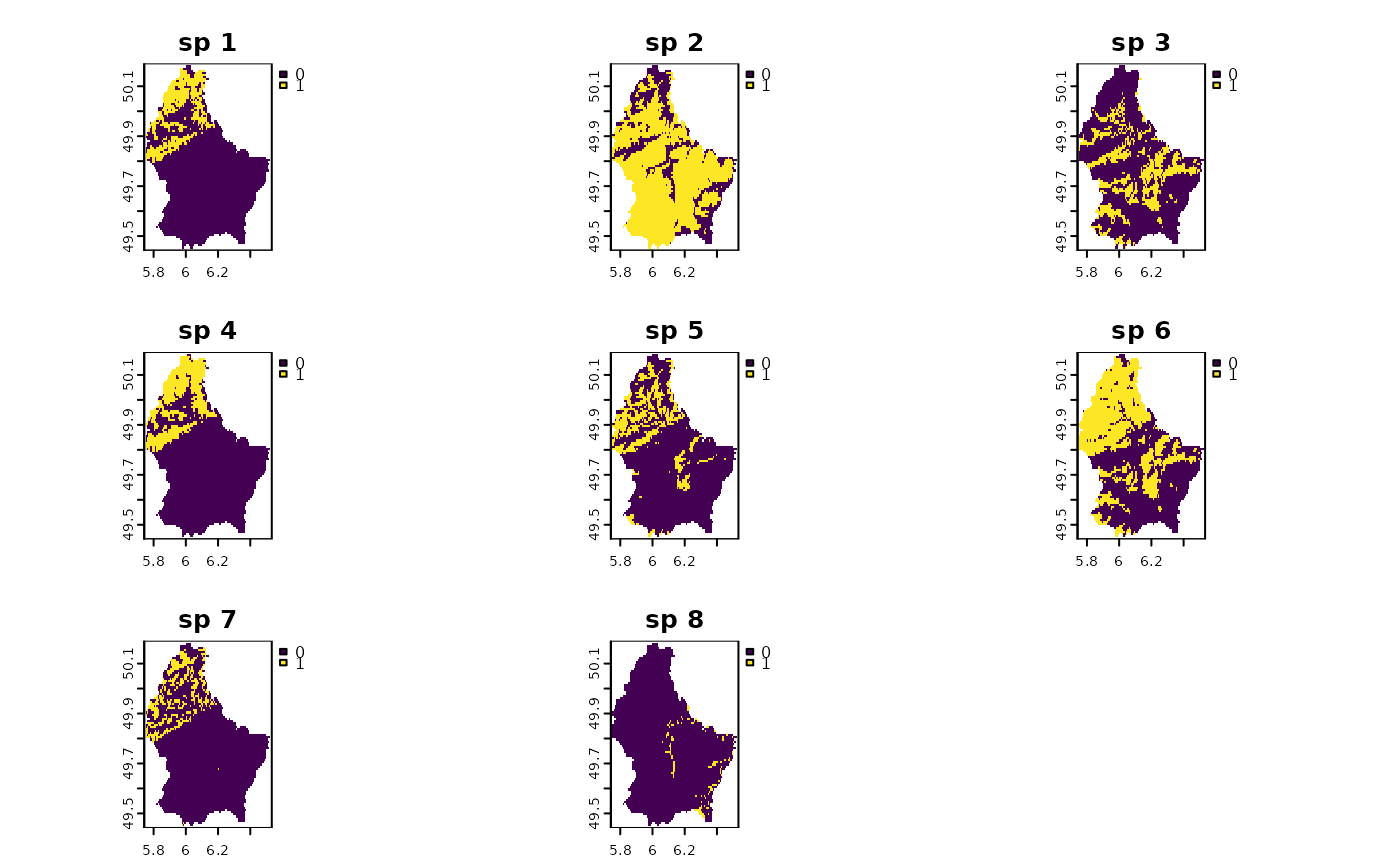 rprobnull <- terra::app(r10,
function(x){
ifelse(is.na(x), NA, 1)
})
# bootstrapping once
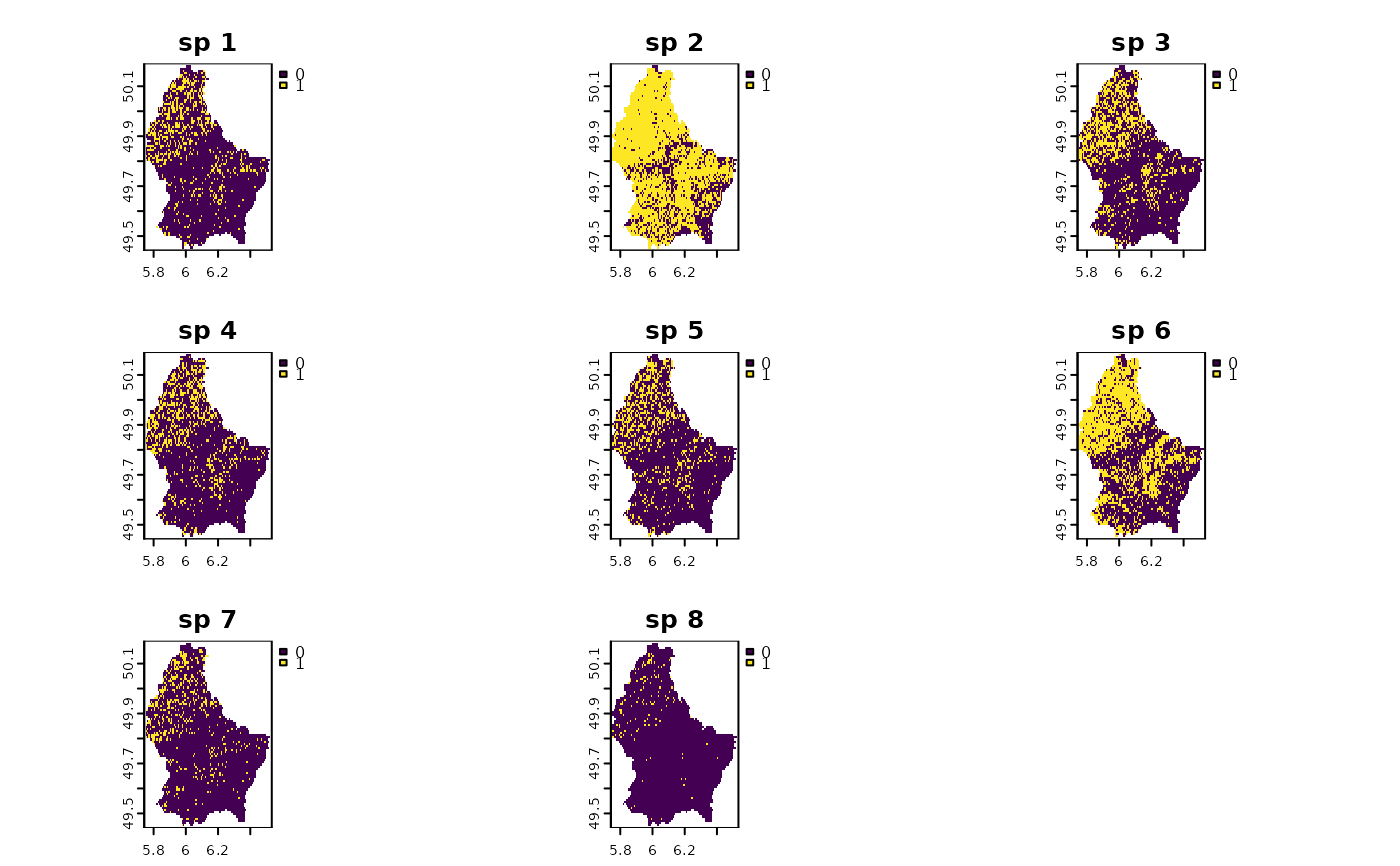
randr10 <- bootspat_ff(r10, rprobnull)
plot(randr10)
rprobnull <- terra::app(r10,
function(x){
ifelse(is.na(x), NA, 1)
})
# bootstrapping once
randr10 <- bootspat_ff(r10, rprobnull)
plot(randr10)
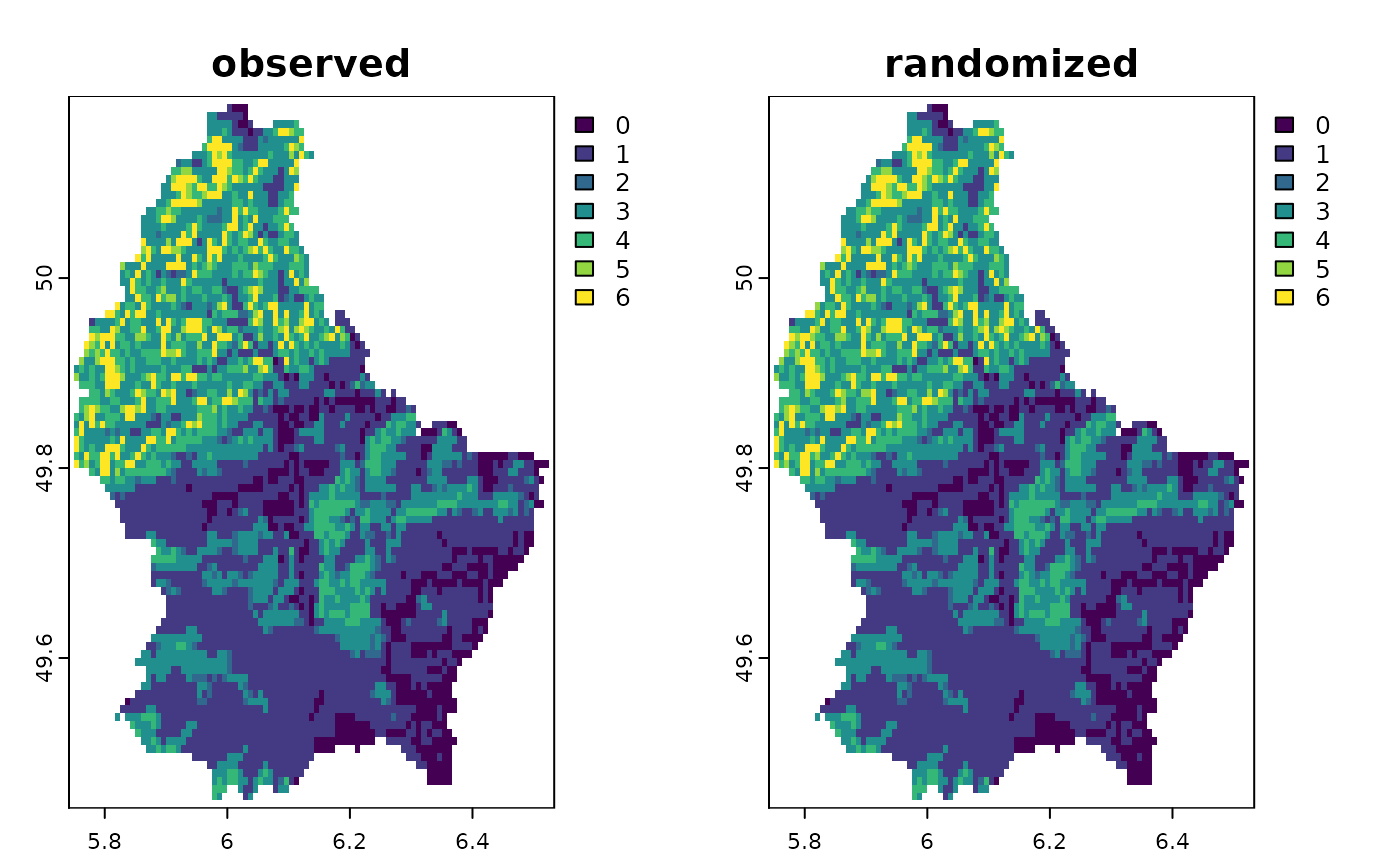
 plot(c(sum(r10), sum(randr10)), main=c("observed", "randomized"))
plot(c(sum(r10), sum(randr10)), main=c("observed", "randomized"))
 plot(sum(r10)-sum(randr10))
plot(sum(r10)-sum(randr10))
 cbind(observed=sapply(r10, function(x)freq(x)[2,3]),
randomized=sapply(randr10, function(x)freq(x)[2,3]))
#> observed randomized
#> [1,] 767 767
#> [2,] 3443 3443
#> [3,] 1175 1175
#> [4,] 889 889
#> [5,] 908 908
#> [6,] 2160 2160
#> [7,] 548 548
#> [8,] 133 125
cbind(observed=sapply(r10, function(x)freq(x)[2,3]),
randomized=sapply(randr10, function(x)freq(x)[2,3]))
#> observed randomized
#> [1,] 767 767
#> [2,] 3443 3443
#> [3,] 1175 1175
#> [4,] 889 889
#> [5,] 908 908
#> [6,] 2160 2160
#> [7,] 548 548
#> [8,] 133 125
